Frattali
Lu frattali è n'uggettu giumetricu particulari. Li frattali janu discrizzioni assai sèmprici, basata supra na seri di trafurmazzioni di nùmmura cumplessi. Lu nomu frattali fu cuniatu dû matimaticu francu-miricanu Benoît Mandelbrot chi cuntribbuìu a fàrili canusciri e a fàrili divintari pupulari.
La sò rapprisintazzioni si carattirizza pi lu fattu ca po ssiri tagghiatu 'nti parti cchiù nichi ca assumigghianu assai a l'inzemi urigginariu ri unni s'accuminzau.
N'autra cosa jèni ca li frattali anu 'na diminziuni ca nun jèni chidda unu s'aspittassi: di solitu nun jè nu nummùru nteru pusitivu.
Infini, 'nta parti viramenti nichi di l'inzemi, l'inzemi stissu cuntìnua a pariri ancora viramenti.
La Curva di Koch
[cancia | cancia lu còdici]
La Curva di Koch jèni n'izempiu semprici di nu frattali.
Ppi prima cosa accumènza ccu na linìa cuntìnua ca vèni ciamata sigmentu di linìa dirìtta.
Appuoi si tagghia a linìa 'nta tri piezzi dâ stissa diminziòni.
Si fanu fora li parti cintrali di 'sti piezzi e si miènti 'nta parti supiriùri dô trianculu ccu lati ca anu a stissa larghizza dâ parti ca si tagghiau fora antura.
Ora aviemu quattru linìi ca si toccanu a l'estremitati.
Ora putiemu fari chiddu ca ficimu â prima linìa a ugnunu dei quattru piezzi: u putièmu fari nu munzieddu di voti ccu tutti i parti ca n'arrestanu duoppu ô travagghiu. Si ci faciemu fari lu travagghiu a nu cumputer (ccu itirazzioni infiniti) finièmu pp'avìri a Curva di Koch.
A lunghizza di 'sta Curva di Koch uttinuta jèni infinita e l'arìa dâ Curva di Koch jèni zeru: e chissu fa miravigghia.
Na linìa di sigmèntu (ccu diminzioni 1) pò aviri na lunghizz di 1, ma avi n'arìa di zero appuntu.
Nu quatràtu ccu latu di lunghizza 1 e larghizza 1 (ccu 2 diminzioni) javi arìa 1 e lunghizza infinita.
Diminziuni Similari
[cancia | cancia lu còdici]Allura a Curva di Koch parissi ssiri cchiu ranni di quarchi cosa di diminziuni 1, e cchiu nica di diminziuni 2.
L'idìa di diminziuni similàri jè di dari 'na diminziù ca dui n miegghiu idèadi lunghìzza o arìa piei frattali.
Picciò, ppi na Curva di Koch, vulissimu 'na diminzioni ca stàpi 'ntra 1 e 2.
A Curva di Koch ppò ssiri tagghiàta 'nta quattru parti, ugnuna diei quali avi dâ rannìzza dill'urigginàli.
I matimatici ciamanu lu nummuru di piezzi ca ppo ssiri tagghiatu nu frattali We call the number of pieces that a fractal can be cut into , e ciamanu a diffirènza di rannìzza .
Sti dui variàbbili i mintiemu 'nta n'iquazzioni:
Unni jèni lu logarìttimu di nu nummuru. Stu nummuru jè ciamatu a Diminziòni di Hausdorff dô frattali.
'Nta Curva di Koch, chissu jèni ..
La Curva di Koch jèni una dei formi cchiu sèmprici di frattali, e jaccussini è viramenti facili calcularasìllu. A sô Diminzioni Similari e a sô Diminziòni di Hausdorff sunu uquali. Chissu nun è o veru ppi frattali cchiu cumpressi.
Lu cioccu di nivi di Koch
[cancia | cancia lu còdici]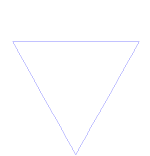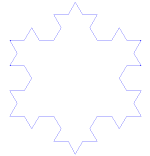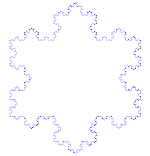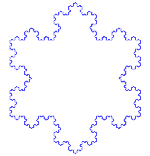
U fioccu di nevi di Koch(o stidda di Koch) è a stissa cosa dâ Curva di Koch iccèttu ca accumènza ccu nu trianculu iquilatiru mmèci di nu sigmèntu di linìa.
Appricazzioni
[cancia | cancia lu còdici]Li frattali janu nu munzieddu d'appricazzioni ppa isempiu 'nta bioluggìa (purmuna, rina, variabbilitati diei pursazzioni di lu cori icc...), 'nta a privsioni diei tirrimoti, 'nta finanza unni è culligata a chiddi ca si ciamanu distribuzzioni a cura pizanti e, 'n giniràli, 'nta fisìca.
Chissu ìnnica ca li frattali avissiru a ssiri sturiati ppi capìri picchi su accusì friquenti 'nta natura.






